1 Boolean and Stone spaces
This is part of a longer thesis
advancing a refutation of strong AI. To
download the thesis visit: -
For an introduction to the work
as a whole visit: -
Introduction
to Poincare’s thesis by Peter Fekete
1.1 Definition,
Boolean space
A topological
space that is compact and totally disconnected is said to be a Boolean space.
1.2 Theorem, existence of Stone space
Let M be the set of maximal ideals of a Boolean algebra B. For any 
define 
. Define a topology T
for M so that arbitrary unions of sets of the form 
are open sets of T. Then 
is a Boolean space in
which the clopen sets of M are the sets . is
called the Stone space of B.
Example
[See example 5 /
7.30] Before proving this, let us
illustrate it with a finite example. In 
the prime ideals
(maximal ideals) are given by
The topology T on M generates the Stone space where the
prime ideals, 
of become its atoms. The atoms constitute a partition of the Stone
space, which is compact and totally disconnected. There is a Boolean algebra which is the power
set 
which is isomorphic to , the original Boolean algebra. The Stone space is isomorphic to but is an inverted
copy of it.
Proof of the theorem
If m is a
maximal ideal then m is a proper ideal; hence 
for some
. To show that 
is a Boolean space we
must show that it is totally disconnected and compact.
1. A space S is totally
disconnected iff for distinct points 
there exists a clopen set 
such that 
and 
. Now suppose that 
are distinct maximal ideals. Then there
is a 
where
and 
. Since 
we have 
but 
. So M is
totally disconnected.
Example
[See example
5.7.30] In we have
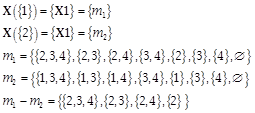
Let 
.
Hence 
.
2. A space S is compact if every
open cover of S has a finite subcover. Let M be
covered by a collection of open sets 
where
. To aim for a
contradiction, suppose M is not covered by some finite subset of . Each 
is a collection of
sets of the form ; hence M can be covered by a collection U of
sets of the form where 
. Then no finite
subset of U covers M. Let 
be any finite subset
of C. Then, because there is no
finite subcover of M we have: -
Thus 
for any . Then the ideal
generated by C is a proper ideal.
Hence, by the Boolean Prime Ideal theorem [7.25 below] there is a
maximal ideal 
containing C. But this applies to any , so 
. Hence M is
not covered by the collection U of open sets, contradicting our
supposition that it was.
The Cantor set is 
. The topology above 
for 
is also a basis of the
Cantor set, and hence shows that the Cantor set is compact. [See 5 / 3.7]
We take the ideal 
of all finite subsets of 
. Then we make a copy
of this and add to each member the “point at infinity” 
, which creates a collection homeomorphic
to all cofinite subsets –
. Together these two
collections cover . Both collections are
independently locally compact. A single
set 
suffices to cover but by the definition
of the topology it must contain some finite subset of as well; all the other
points may be covered by a collection of
members of . Since this
collection is locally compact there is a finite subcover
of it. Let this finite subcover be denoted 
; then 
is a finite cover of . The set acts as the skeleton
of the Cantor set; hence the Cantor set inherits its compactness from . One-point compactification is an analogue of the Heine-Borel theorem – in its turn equivalent to the Completeness
Axiom. The compactness of the Cantor
set also follows from Tychanoff’s theorem. (For further comment see Givant and Halmos [2009] p. 305.)
1.3 Tychonoff’s theorem
Every product of
compact spaces is compact. Conversely,
if a product of non-empty spaces is compact then each of its factors is
compact.
1.4 A puzzel and its resolution
Notwithstanding the remarks already
made above, the compactness property for the Stone space has an air of paradox
that should be investigated further. For
finite Boolean lattices compactness follows automatically, but in the infinite
case there are prima facie reasons why the Stone space, here 
, should not be compact, that the theorem
refutes. To explain: the Stone space, M,
is infinitely partitioned into atoms 
which are separated
from each other, disjoint and taken together the space is totally disconnected,
as shown in the first part of the theorem.
Each atom is apparently related to some element so that we have ; also B is infinite.
The definition of compactness requires that every open cover of a
compact space has a finite subcover. To show that X is not compact
one must find an example of a cover for X that is not finite; so a space
is not compact if there exists just one
infinite open cover for it, which makes the meaning clear.
Example
The open interval 
is not compact in 
. For each member of
the collection 
where 
is open in ; also 
. But there is no
finite subcollection of this collection that covers .
Following the example, one is inclined
to conclude: surely the collection is an infinite
open cover for ? Examining the proof
of the theorem closely we see that the crucial step when we are lead out of
this conclusion occurs when the Boolean Prime Ideal theorem is cited to
establish the existence of a maximal ideal 
for any subset of B. This theorem in turn rests upon the Axiom of
Choice (specifically in the form of Zorn’s Lemma). The Axiom of Choice functions as a species of
completion axiom; it is this principle that embeds the possibly non-atomic
lattice B into a complete atomic lattice. Specifically, in the case of the Cantor
set, 
, the ideal 
of all
finite subsets of is extended to
a maximal ideal 
, which becomes at atom of the Stone space and corresponds to
a maximal element 
. (Proven below 2.1 and see also
5.7.41/42) The Stone space of the Cantor
set is also isomorphic to the Cantor set again, 
. Since the two sets
are isomorphic, though inverted, there must be an element in corresponding to this atom 
, which is an atom in X. Since 
is an inverted copy of
X, this must be 
. Suppose now we wish
to make an infinite open cover for X.
Then that must include the ideal ; also 
is included in every
infinite open cover for X. But is the infimum in 
of the set of all cofinite subsets of 
which includes every
infinite subset of . Hence, when is subtracted from the
cover, there remains only finite subsets of , which because it contains only finite subsets must be
compact – i.e. have a finite subcover. Thus, it is the addition of to
and the correspondent
addition of to
that makes both
compact. Since both elements belong
to both any complete infinite Boolean algebra B and its Stone space 
has a corresponding
maximal filter 
and a maximal ideal where
.
This is an exact analogy with the Heine-Borel
theorem which renders the interval 
compact by adding the
neighbourhood of 1 to the locally compact subset 
and thus acts as a
one-point compactification of it. In the Cantor set, , 
represents the
neighbourhood of 0 and the neighbourhood of 1. The addition of to
completes it by
embedding in 
and allowing a
complete set of atoms for .
1.5 Result
The clopen subsets of a Boolean space X form a field of
sets.
1.6 Definition,
dual Boolean algebra
The field of clopen subsets of a Boolean space X is called the dual
(Boolean) algebra, denoted 
.
1.7 Result, Stone
duality
The dual algebra of the field of clopen subsets of is isomorphic to the
original algebra X. (Proof, Mendelson [1970] p.171) Additionally, X and are homeomorphic.
(Proof, Mendelson [1970] p.171)
I remark on the subtle difference
between this theorem and the preceding Theorem 1.2 demonstrating the existence
of the Stone space. Here we start with a
Boolean space X and construct its dual algebra . We then construct
the Stone space, , of this dual and the claim is that 
. In the preceding
result we start with a Boolean space B and construct its Stone
space. A relation of isomorphism does
not necessarily exist between
B and this
Stone space . This latter case is
illustrated by the relation between the Boolean algebra, 
, of all finite and cofinite
subsets of and the Cantor set, . The two are not isomorphic, but the
Cantor set is the Stone space of .
This is part of a longer thesis
advancing a refutation of strong AI. To
download the thesis visit: -
For an introduction to the work
as a whole visit: -
Introduction
to Poincare’s thesis by Peter Fekete