7 Ideals in a Boolean algebra
This
is part of a longer thesis advancing a refutation of strong AI. To download the thesis visit: -
For an introduction to the work as a
whole visit: -
Introduction
to Poincare’s thesis by Peter Fekete
Recall the fundamental definitions for
a lattice.
![]()
Filters (up-sets) and
ideals (down-sets) were introduced earlier [4.6.1]. Filters are very important for analytic logic
built over a lattice since the filter of a lattice point ![]() is synonymous to the
consequences of that lattice point:
is synonymous to the
consequences of that lattice point: ![]() . Filters and ideals
are dual concepts, and in the context of Boolean algebras it is usual to
develop the theory primarily for ideals and argue by duality that the same
theory applies to filters.
. Filters and ideals
are dual concepts, and in the context of Boolean algebras it is usual to
develop the theory primarily for ideals and argue by duality that the same
theory applies to filters.
7.1 Definition, ideal
Let ![]() be a Boolean
algebra. Let
be a Boolean
algebra. Let ![]() be a non-empty subset
of B. The J is said to be
an ideal of B if
be a non-empty subset
of B. The J is said to be
an ideal of B if
1. ![]()
2. ![]()
Examples
![]() and B are both
ideals of a Boolean algebra B.
and B are both
ideals of a Boolean algebra B.
7.2 Definition, proper
ideal
Every ideal of a Boolean algebra B, different from B
is said to be a proper ideal of B.
7.3 Result
Let J be an ideal of a Boolean algebra B,
let ![]() and
and ![]() , then
, then ![]() .
.
What this result
emphasises is that everything that lies below a point ![]() in an ideal also lies
in the ideal J, and this is why they are called down sets. This also means that the natural way to
picture an ideal is as the down set of some element of the lattice
in an ideal also lies
in the ideal J, and this is why they are called down sets. This also means that the natural way to
picture an ideal is as the down set of some element of the lattice
![]() , so that the ideal is generated from the top down. As it happens, not all ideals can be
generated in this way. When they are,
they are called principal ideals.
, so that the ideal is generated from the top down. As it happens, not all ideals can be
generated in this way. When they are,
they are called principal ideals.
7.4 Definition,
principal ideal
![]() in the above result
is said to be a principal ideal of B.
in the above result
is said to be a principal ideal of B.
Examples
1. ![]() is
a proper ideal .
is
a proper ideal .
2. J is a proper ideal iff ![]() .
.
Principal ideals are
defined by “topmost elements”. To say
that an ideal is principal is to say that there is a “topmost” that is
principal element in the lattice and that the ideal comprises every other
element in the lattice that lies below this. That is,
an ideal J is principal in Boolean algebra B iff
![]() . (The term “topmost”
is not standard and is introduced here to help visualise the concept.)
. (The term “topmost”
is not standard and is introduced here to help visualise the concept.)
7.5 Result,
principal ideal
Let ![]() be an element of a
Boolean algebra B. Then the set
be an element of a
Boolean algebra B. Then the set ![]() is an ideal of B. (Proof, Mendelson
[1970] p. 144)
is an ideal of B. (Proof, Mendelson
[1970] p. 144)
In a finite Boolean
algebra every ideal must be principal.
This follows immediately from the definition of an ideal where we have ![]() and in a finite Boolean algebra every set of lattice points
has a join.
and in a finite Boolean algebra every set of lattice points
has a join.
7.6 Properties of
principal ideals
(Mendelson [1970] examples 5.9,5.10)
1. Let
A be a non-empty set and ![]() the Boolean algebra on A. Then the atoms of
the Boolean algebra on A. Then the atoms of ![]() are the singleton sets
are the singleton sets
![]() where
where
![]() . Hence any maximal
principal ideal consists of all subsets X of A such that
. Hence any maximal
principal ideal consists of all subsets X of A such that ![]() .
.
Example
![]() is
the algebra of subsets of
is
the algebra of subsets of ![]() . The atoms are
. The atoms are ![]() and by deleting any
one member of A, we obtain a maximal principal ideal. These are
and by deleting any
one member of A, we obtain a maximal principal ideal. These are ![]() .
.
2. In
any finite Boolean algebra every maximal ideal is a principal ideal.
In an infinite
Boolean algebra not every infinite set of lattice points need have a join, or
alternatively, that join need not be contained in the ideal. So to consider non-principal ideals we must
be discussing an infinite lattice. The
paradigm of a non-principal idea is the ideal of all finite subsets of ![]() , which is a subset of the Cantor set,
, which is a subset of the Cantor set, ![]() . We can see
automatically that this subset is (a) an ideal and (b) cannot be
principal. It is an ideal because for
every two finite subsets of
. We can see
automatically that this subset is (a) an ideal and (b) cannot be
principal. It is an ideal because for
every two finite subsets of ![]() there is a join; it
cannot be principal because there cannot be a single finite subset of
there is a join; it
cannot be principal because there cannot be a single finite subset of ![]() that contains every
other finite subset of
that contains every
other finite subset of ![]() . This is a consequence of the
manner in which the ideal is generated from the bottom upwards as a potentially
infinite structure. As it follows
that in any infinite set not all ideals are principal it also follows that
there must be some other method of generating an ideal – one that proceeds from
the “bottom up” just as these remarks suggest.
. This is a consequence of the
manner in which the ideal is generated from the bottom upwards as a potentially
infinite structure. As it follows
that in any infinite set not all ideals are principal it also follows that
there must be some other method of generating an ideal – one that proceeds from
the “bottom up” just as these remarks suggest.
7.7 Result,
generator
Let ![]() be a subset of a
Boolean algebra B. Then the
intersection
be a subset of a
Boolean algebra B. Then the
intersection ![]() such that
such that ![]() is an ideal containing
X,
is an ideal containing
X, ![]() , is itself an ideal such that
, is itself an ideal such that ![]() .
.
7.8 Definition,
generator
The set X corresponding to the ideal J in the
above result is said to be the generator of J. We write this ![]() .
.
7.9 Theorem
Let X be any subset of a Boolean algebra, B,
then ![]() is the set
is the set
![]() .
.
(Proof, Mendelson [1970] p. 144)
7.10 Theorem
Let X be any subset of a Boolean algebra, B,
then ![]() is the set
is the set
![]()
(Proof, Mendelson [1970] p. 144)
To say
that an ideal is principal in a Boolean algebra:![]() means that this
principal element u is the disjunction of elements of a set X
that generates J. In other words,
to say an ideal J is principal is to say that it has a set X that
generates J such that
means that this
principal element u is the disjunction of elements of a set X
that generates J. In other words,
to say an ideal J is principal is to say that it has a set X that
generates J such that ![]() and
and
![]() ,
, ![]() . This is the result
that clarifies the meaning of generators in this context. The generators could be atoms, if atoms
exist. If atoms do not exist, take any
subset X and form the disjunction of its elements
. This is the result
that clarifies the meaning of generators in this context. The generators could be atoms, if atoms
exist. If atoms do not exist, take any
subset X and form the disjunction of its elements![]() . Then
. Then ![]() is the ideal that lies
below this topmost element
is the ideal that lies
below this topmost element
7.11 Result
Let X be any subset of a Boolean algebra, B,
then ![]() is proper ideal of B
iff
is proper ideal of B
iff
![]() where
where ![]() .
.
(Proof Mendelson [1970] p. 144)
7.12 Result
(Mendelson [1970] p. 160) Let B
be an atomic Boolean algebra. Then very
element ![]() is the l.u.b. (supremum) of the set: -
is the l.u.b. (supremum) of the set: -
![]() and
x is not the l.u.b. of any proper subset of
and
x is not the l.u.b. of any proper subset of ![]() .
.
Proof
We have ![]() , so the condition
, so the condition ![]() implies x is an
upper bound for
implies x is an
upper bound for ![]() .
.
Let z be an upper bound of ![]() such that
such that ![]() .
.
Then ![]() .
.
Since B is atomic there exists an atom
![]() .
.
Therefore, ![]() and
and ![]() .
.
Also ![]() . But as z is
an upper bound for
. But as z is
an upper bound for ![]() , then
, then ![]() . Therefore,
. Therefore, ![]() which
is a contradiction, since b is an atom. Therefore, z must be an upper bound of
which
is a contradiction, since b is an atom. Therefore, z must be an upper bound of
![]() such that
such that ![]() , an so x must be the l.u.b.
of
, an so x must be the l.u.b.
of ![]() . (For the second half
of this proof, Mendelson [1970] p. 160)
. (For the second half
of this proof, Mendelson [1970] p. 160)
What this means is
that every set of atoms generates an ideal. Ideals are generalised Boolean algebras
embedded in a larger Boolean algebra.
7.13 Definition, subalgebra
(Givant and Halmos [2009] p. 74)
A Boolean subalgebra
of a Boolean algebra A is a subset B of A such that B
together with the distinguished elements and operations of A (restricted
to the set B) is a Boolean algebra.
The algebra A is called a Boolean extension of B.
7.14 Definition, generalised Boolean algebra
(Birkhoff [1940] who
attributes this to Stone)
A generalised Boolean algebra is an algebra that
has no largest element 1, and hence is not a complemented lattice. However, it is a relatively complemented,
distributive lattice. [See 5.8 above]
Thus, we have ideals
that are not principal. This, therefore,
invites the following definition: -
7.15 Definition, maximal
ideal
An ideal M of a Boolean algebra B is said to
be maximal if M is a proper ideal and if there is no proper ideal
J of B such that ![]() .
.
This definition is
essential in order to distinguish two concepts of “maximality”
– the first is the natural concept of principal ideal where the ideal may be thought
of as generated top down from a “topmost” element; the second arises from the
bottom up approach as a species of limit – it is the largest ideal that can be
generated from the bottom up without reaching the topmost element of the
lattice as a whole, that is 1. If
the lattice is atomic then this makes the distance of 1 above M just
1. The distance from an atom to 0
is also just 1. This last remark makes
it clear that maximal ideals are to 1 in the lattice as atoms
are to 0.
It follows from the
definition of an ideal that ![]() is an ideal in
is an ideal in ![]() , but we have not proven
that
, but we have not proven
that ![]() is a maximal ideal. It is known that it is impossible to
do this in ZF set theory, and that its proof requires
the Axiom of Choice [3.12 above], specifically in its equivalent form of Zorn’s
lemma: -
is a maximal ideal. It is known that it is impossible to
do this in ZF set theory, and that its proof requires
the Axiom of Choice [3.12 above], specifically in its equivalent form of Zorn’s
lemma: -
7.16 Zorn’s lemma
Let X be a partially ordered set in which every chain (i.e totally ordered subset) has an upper bound, then X
possesses a maximal element.
7.17 Definition, subset
chain
Let S be a set of
sets. Then a ![]() -chain in S is a subset of S such that if
-chain in S is a subset of S such that if ![]() and
and ![]() where
where![]() , then either
, then either ![]() or
or ![]() .
.
More generally
Let R be a binary relation on a set W. Then an R-chain in W is a
subset of W on which R is transitive, connected and antisymmetric.
7.18 Definition,
technical variant of Zorn’s lemma
Let S be a set of sets such that for every ![]() -chain C in S,
the union
-chain C in S,
the union ![]() is also in S.
Then there is a C-maximal set M in S.
is also in S.
Then there is a C-maximal set M in S.
7.19 Definition, prime
ideal
Let J be an ideal of a Boolean algebra B. Then J is said to be prime iff for all ![]() such that
such that ![]() and
and ![]() we have
we have
![]() .
.
7.20 Theorem
A proper ideal J in a Boolean algebra B
is maximal iff it is Boolean prime ideal.
(Proof, Mendelson [1970] p. 145)
So there
is some duplication of terminology here since prime ideal means the same as maximal proper ideal.
This means that in an infinite Boolean algebra, prime = maximal. Not all maximal ideals are principal: the join of an infinite
set does not necessary exist in the lattice.
7.21 Maximal ideal
theorem
Let J be a proper ideal of a Boolean algebra B. Then there is a maximal ideal M in B
such that ![]() . This means that
every proper ideal can be extended to a maximal ideal. (Note underlining.)
. This means that
every proper ideal can be extended to a maximal ideal. (Note underlining.)
Proof
Let J be a proper ideal of a Boolean
algebra B. Let Z be the
class of all proper ideals K such that ![]() . Let C be any
. Let C be any ![]() -chain in Z.
Then
-chain in Z.
Then ![]() is a proper ideal
containing J. However, this is
automatic, because by definition every element in M contains J,
so the union of all such ideals in C must contain J. Hence, by Zorn’s lemma there is a maximal set
M in Z such that
is a proper ideal
containing J. However, this is
automatic, because by definition every element in M contains J,
so the union of all such ideals in C must contain J. Hence, by Zorn’s lemma there is a maximal set
M in Z such that ![]() . Furthermore, M
must be a maximal ideal in B. To
show this, let
. Furthermore, M
must be a maximal ideal in B. To
show this, let ![]() be a proper ideal such
that
be a proper ideal such
that ![]() . Then
. Then ![]() so
so ![]() .
.
7.22 Corollary
Let ![]() be the Boolean algebra of all subsets of the
infinite set
be the Boolean algebra of all subsets of the
infinite set ![]() . Let
. Let ![]() be the ideal of all
finite subsets of
be the ideal of all
finite subsets of ![]() . Then
. Then ![]() can be extended to a
maximal ideal
can be extended to a
maximal ideal ![]() .
.
7.23
(+) The Maximal
idea theorem is the central result of representation theory
This is the central result of the representation theory of
infinite Boolean lattices. The actual representation theorem follows below [7.29 below],
and is also called the Prime Ideal theorem. In essence, these are all the same theorem
and are consequences of the application of the Axiom of Choice to the ideal ![]() to extend it to a
maximal ideal
to extend it to a
maximal ideal ![]() . It is this result
that justifies the distinction we have drawn between the two concepts, and also
indicates that they are separate structures.
. It is this result
that justifies the distinction we have drawn between the two concepts, and also
indicates that they are separate structures.
I have taken the statement of this
theorem from Mendelson [1970]. However, the expression “in B” in it
(underlined above) [Second line 7.21] is ambiguous. ![]() is
an ideal in B (which is here
is
an ideal in B (which is here ![]() ) but its maximal ideal,
) but its maximal ideal, ![]() , in effect demonstrates that B (where
, in effect demonstrates that B (where![]() ) is a complete Boolean algebra in its own right.
) is a complete Boolean algebra in its own right. ![]() is
a Boolean algebra of which
is
a Boolean algebra of which ![]() is an ideal, but
is an ideal, but ![]() is not a maximal ideal
of
is not a maximal ideal
of ![]() ;
; ![]() belongs to the Cantor
space,
belongs to the Cantor
space, ![]() of which
of which ![]() is a sub-algebra. Hence, the Axiom of Choice is allowing us to
extend and complete
is a sub-algebra. Hence, the Axiom of Choice is allowing us to
extend and complete ![]() by embedding it in
by embedding it in ![]() .We have
.We have ![]() as an unbounded
sequence. Just like
as an unbounded
sequence. Just like ![]() it has no maximal
element and satisfies the Archimedean property [See 3.1 above]. And yet, by
applying Zorn’s lemma to it, we have demonstrated the existence of
it has no maximal
element and satisfies the Archimedean property [See 3.1 above]. And yet, by
applying Zorn’s lemma to it, we have demonstrated the existence of ![]() . Compare with
. Compare with ![]() , so that
, so that ![]() . We have
. We have ![]() , so that
, so that ![]() remains unbounded
above, but
remains unbounded
above, but ![]() , so that it does have a maximum. By a similar argument there is a sequence of
ideals
, so that it does have a maximum. By a similar argument there is a sequence of
ideals ![]() of which
of which ![]() is the last with
is the last with ![]() as an unbounded
sequence, so that
as an unbounded
sequence, so that ![]() yet
yet ![]() .
.
Under the
hypothesis ![]() the application of
Zorn’s lemma in the Maximal ideal theorem leads to an actual contradiction
since it ascribes a maximum to a sequence
the application of
Zorn’s lemma in the Maximal ideal theorem leads to an actual contradiction
since it ascribes a maximum to a sequence ![]() that could not have one. The “paradox” is resolved by
that could not have one. The “paradox” is resolved by ![]()
![]() so the sequence on
which Zorn’s lemma is applied in this case is not
so the sequence on
which Zorn’s lemma is applied in this case is not ![]() but
but ![]() .
.
Zorn’s lemma is
also used in the construction of the one-point compactification
of ![]() [Result 3.22 above],
and it seems that its function (as with its equivalent Axiom of Choice) is to
assert the existence of an actually infinite complete partition of the
interval.
[Result 3.22 above],
and it seems that its function (as with its equivalent Axiom of Choice) is to
assert the existence of an actually infinite complete partition of the
interval.
7.24 Result
Every proper ideal J of a Boolean algebra
B is equal to the intersection H of all maximal ideals containing
it. (Proof Mendelson
[1970] 5.34)
This means that every
proper ideal can be extended to a maximal ideal. Given the equivalence: maximal proper ideal ![]() prime ideal, this is
equivalent to: -
prime ideal, this is
equivalent to: -
7.25 Prime ideal
theorem
Let J be a proper ideal of a Boolean
algebra B. Then there is prime
ideal in B that contains J.
7.26 Lemma,
constructing ideals by adjoining elements
1. Let J
be an ideal of a Boolean algebra B and let ![]() . Then
. Then ![]() is an ideal consisting
of all elements of the form
is an ideal consisting
of all elements of the form ![]() where
where ![]() and
and ![]() . (Proof Mendelson [1970] p.145)
. (Proof Mendelson [1970] p.145)
2. Let J
be an ideal of a Boolean algebra B and let ![]() . Then the ideal
. Then the ideal ![]() is a proper ideal iff
is a proper ideal iff ![]() for all
for all
![]() . That is, for all
. That is, for all ![]() , iff
, iff ![]() . (Proof Mendelson [1970] p.145)
. (Proof Mendelson [1970] p.145)
This is a
kind of technical lemma required in the proof of the theorem below: -
7.27 Theorem, maximal
ideals as partitions
Let M be a proper ideal of
a Boolean algebra, B. Then M
is maximal iff for any ![]() either
either ![]() or
or ![]() .
.
1. Suppose M is maximal and ![]() . Let
. Let ![]() . This defines an ideal
such that
. This defines an ideal
such that ![]() . Since M is
maximal, this entails
. Since M is
maximal, this entails ![]() . Hence by the lemma
above
. Hence by the lemma
above ![]() for some
for some
![]() . Since M is an
ideal this entails
. Since M is an
ideal this entails ![]() .
.
2. Conversely,
suppose either ![]() or
or ![]() for all
for all
![]() . Let
. Let ![]() where J is an
ideal. Suppose
where J is an
ideal. Suppose ![]() . This means
. This means ![]() and
and ![]() , hence
, hence ![]() . Then
. Then
![]() . Hence
. Hence
![]() , which entails that M is maximal.
, which entails that M is maximal.
7.28 Corollary
(Givant and Halmos [2009] p. 173, also Mendelson
[1970] p.149)
Let J be any proper ideal of a Boolean
algebra B. For every element p
in B that does not belong to J there exists a maximal ideal M
that includes J but does not contain p.
Proof
The ideal N generated by ![]() is proper. Then the maximal ideal theorem entails that
there is a maximal ideal that contains N and hence also M. As it is a maximal ideal that contains
is proper. Then the maximal ideal theorem entails that
there is a maximal ideal that contains N and hence also M. As it is a maximal ideal that contains ![]() it cannot contain p.
it cannot contain p.
7.29 Corollary, Boolean
representation theorem (Birkhoff)
Every Boolean algebra is isomorphic to a field of sets.
Proof idea
For any Boolean algebra B there is an isomorphism
into the power set ![]() of the set of all
maximal ideals M in B. The
image of this isomorphism is a field of sets contained in
of the set of all
maximal ideals M in B. The
image of this isomorphism is a field of sets contained in ![]() .
.
Proof
Let B be any Boolean algebra. Let m denote
a maximal ideal. Let M denote the
set of all maximal ideals. For ![]() let
let
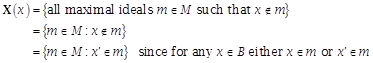 .
.
Then ![]() is the set of all
maximal ideals of B and
is the set of all
maximal ideals of B and ![]() . We also have
. We also have
1. ![]() .
.
2. ![]() .
.
3. ![]() as
every maximal ideal contains either x or
as
every maximal ideal contains either x or ![]() .
.
4. ![]()
Let m denote a maximal
ideal. That is ![]() .
.
![]() since
since ![]() . Similarly,
. Similarly, ![]() since
since
![]() . Hence,
. Hence, ![]() . Conversely
. Conversely
![]() . Thus, by
contraposition
. Thus, by
contraposition
![]() . Hence
. Hence
![]() .
.
Hence X is an isomorphism from B into ![]() , the set of all subsets of the set M of all maximal
ideals.
, the set of all subsets of the set M of all maximal
ideals.
7.30 Finite example
The Boolean algebra ![]() : -
: -
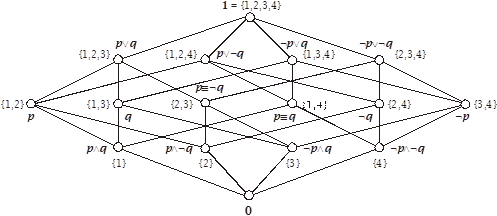
The maximal ideals (Boolean primes) are
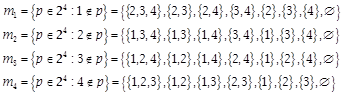
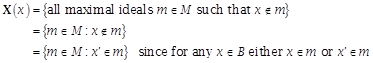
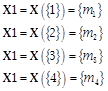
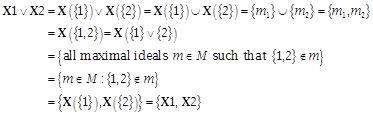
Likewise
![]()
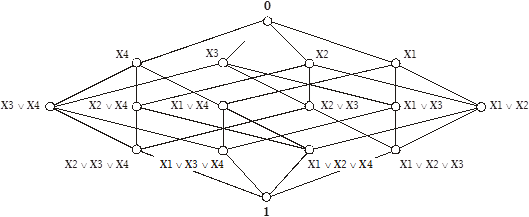
Compare this with

and
![]()
All of these express
the same underlying facts.
For the finite case
we generate the Boolean algebra upwards as the power set of the set of its
atoms, and the construction involving maximal ideals is not necessary. For infinite cases this is not possible. Therefore, we assume that the
corresponding maximal ideals exist, which we justify by the Axiom of Choice,
and generate the complete Boolean algebra downwards as a algebra of maximal ideals. Each maximal ideal defines an atom of this
dual algebra for which the set of atoms is a basis.
7.31 Result
Every proper ideal J of a Boolean algebra
B is equal to the intersection H of all maximal ideals containing
it.
Proof
By
the maximal ideal theorem there is a maximal ideal containing J. Then ![]() . To show that
. To show that ![]() , let
, let ![]() . By the lemma on constructing ideals by adjoining
elements,
. By the lemma on constructing ideals by adjoining
elements, ![]() is a proper ideal. By
the maximal ideal theorem, there is a maximal ideal M such that
is a proper ideal. By
the maximal ideal theorem, there is a maximal ideal M such that ![]() . Whence
. Whence ![]() and
and ![]() . But H is the
intersection of all maximal ideals containing J, hence
. But H is the
intersection of all maximal ideals containing J, hence ![]() and
and ![]() .
.
7.32 Result
A
Boolean algebra B is isomorphic to a field ![]() of all subsets of a non-empty set X iff B is complete and completely distributive.
(Proof Mendelson [1970] p.174)
of all subsets of a non-empty set X iff B is complete and completely distributive.
(Proof Mendelson [1970] p.174)
7.33 Alternative
approaches to the Boolean representation theorem
The approach here is
to derive the Boolean representation theorem by the following route: (1)
Definition of maximal ideals; (2) Zorn’s lemma to establish the maximal ideal
theorem; (3) Maximal ideals acting as a basis for the Boolean algebra taking
the place of atoms; (4) Boolean representation theorem as equating the Boolean
algebra in the field of sets generated by that basis.
It is as well to note
that there is an alternative approach to this theorem, which is one that might
also be more appropriate to a universal algebra[1]. (1) Definition of homomorphisms;
(2) Definition of quotient algebras; (3) Decomposition of algebras into factors
of indecomposable algebras; (4) Use of Zorn’s lemma to establish Birkhoff’s theorem: Every algebra A
is isomorphic to a subdirect product of subdirectly irreducible algebras that are homomorphic images of A.
The first approach is
due to Stone and the second to Birkhoff. The two approaches are equivalent.
7.34 Outline of the
“universal” approach to the Boolean / Stone representation theorem
An
algebra A is directly
indecomposable if A is not isomorphic to a direct product of two
nontrivial algebras.
7.35 Theorem
Every finite algebra is isomorphic to a direct product of
directly indecomposable algebras.m For Boolean algebras
the only directly indecomposable algebra is ![]() . So
all Boolean algebras are built up as products of this unit. Although every finite
algebra is isomorphic to a direct product of directly indecomposable
algebras, the same does not hold for infinite algebras in general. To find building blocks for algebras we
therefore require the notion of a subdirect product.
. So
all Boolean algebras are built up as products of this unit. Although every finite
algebra is isomorphic to a direct product of directly indecomposable
algebras, the same does not hold for infinite algebras in general. To find building blocks for algebras we
therefore require the notion of a subdirect product.
7.36 Definition, subdirect product
An algebra A is a subdirect
product of an indexed family ![]() of algebras if
of algebras if
(i) ![]()
(ii) ![]() .
.
7.37 (+) Result
The Cantor set ![]() is the direct product
of
is the direct product
of ![]() copies of
copies of ![]() , but
, but ![]() , the Boolean algebra of all finite subsets of
, the Boolean algebra of all finite subsets of ![]() , is not the direct product of any denumerable number of
copies of 2. It is contained in
, is not the direct product of any denumerable number of
copies of 2. It is contained in ![]() as a subfield.
as a subfield.
Proof
Suppose ![]() is the direct product
of copies of 2. Either
is the direct product
of copies of 2. Either![]() is the direct product of a finite copies of 2 or of infinite. If infinite, then
is the direct product of a finite copies of 2 or of infinite. If infinite, then ![]() which is false,
because
which is false,
because ![]() is a proper subset of
is a proper subset of ![]() . If finite, then
. If finite, then ![]() is finite, which is
too small.
is finite, which is
too small.
As an algebra ![]() lies somewhere between
lies somewhere between
![]() where k is any
integer and
where k is any
integer and ![]() . This makes it the subdirect product of 2.
. This makes it the subdirect product of 2.
7.38 Theorem (Birkhoff)
Every algebra A is isomorphic to a subdirect
product of subdirectly irreducible algebras that are homomorphic images of A.
Notes
The proof of this requires Zorn’s lemma.
7.39 Representation of
Boolean prime ideals in the lattice of prime divisors
The
definition of an ideal in the language of a Boolean ring becomes, ![]() . This makes
membership of an ideal appear as a divisibility property. By contraposition
. This makes
membership of an ideal appear as a divisibility property. By contraposition ![]() . A Boolean prime is
equivalent to a composite number that has a unique prime factorisation. The duality principle [4.2.5] allows for the
interchange of ideals for filters; this means that to each Boolean prime ideal
there is a Boolean prime filter.
In the lattice of divisors, these Boolean prime filters actually are
prime numbers.
. A Boolean prime is
equivalent to a composite number that has a unique prime factorisation. The duality principle [4.2.5] allows for the
interchange of ideals for filters; this means that to each Boolean prime ideal
there is a Boolean prime filter.
In the lattice of divisors, these Boolean prime filters actually are
prime numbers.
7.40 Example
As the following finite example illustrates,
this reverses the usual definition of prime and composite.
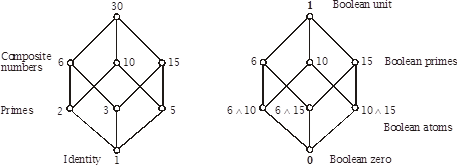
7.41 Elements in a
complete Boolean algebra
The
combination of (1) ![]() , (2) the Axiom of choice making
, (2) the Axiom of choice making ![]() and
and ![]() into sets, (3) the
extension of the power set operation to these results, (4) the definition of
into sets, (3) the
extension of the power set operation to these results, (4) the definition of ![]() and (5)
and (5) ![]() together justify the
assertion
together justify the
assertion ![]()
![]() . The status of
. The status of ![]() in this
needs to be clarified. We have
in this
needs to be clarified. We have ![]()
![]() , which indicates that
, which indicates that ![]() is not an element or
atom of the partition of
is not an element or
atom of the partition of ![]() but a collection of
them:
but a collection of
them: ![]() ;
; ![]() is not a lattice point
of
is not a lattice point
of ![]() . Since the complete
algebra
. Since the complete
algebra ![]() contains all infinite
meets and joins,
contains all infinite
meets and joins, ![]() is a lattice point of
this algebra, just as all its subsets are.
is a lattice point of
this algebra, just as all its subsets are.
7.42 (+) Definition,
maximal “element”
![]() has
no maximum in itself. It is not a
principal ideal in
has
no maximum in itself. It is not a
principal ideal in ![]() . This is because
. This is because ![]() has no maximum – it is
unbounded. However, within
has no maximum – it is
unbounded. However, within
![]() ,
, ![]() is bounded above, and
we say that
is bounded above, and
we say that ![]() is its maximal ideal; we define
is its maximal ideal; we define ![]() to be such that
to be such that ![]() and say that it is its
maximal element.
and say that it is its
maximal element.
An incomplete algebra
is one in which not all infinite meets and joins exist. Hence, there are ideals in such an algebra that are not principal. When the algebra is extended to a complete
algebra X, in X all ideals are principal. Hence a maximal element is a principal
element that is a member of a complete algebra but not a member of its
incomplete embedding.
This result is consistent with
Rubin’s proposition [3.18 above] – yet another version of the Axiom of Choice –
which states that the Axiom of Choice is equivalent to the statement, “The
power set of every ordinal is well-orderable”; ![]() is not an ordinal, but
under the Axiom of Choice it becomes an ordered set, and hence similar
[Defined, Chap.2 / 2.8.3] to an ordinal; then
is not an ordinal, but
under the Axiom of Choice it becomes an ordered set, and hence similar
[Defined, Chap.2 / 2.8.3] to an ordinal; then ![]() is also well-ordered.
is also well-ordered.
The role of the
maximal “element” is analogous to the role played by a real number in
its relation to an infinite sequence of rational numbers as in the
Dedekind cut or any other definition of completeness. Just as ![]() is not an
element of the sequence of rational numbers that defines it, so too the maximal
“element” may or may not be an element of the ideal of which it is the supremum. When it is
not, I shall also call such an element a boundary element. In the paradigmatic case of the ideal of all
finite subsets of some infinite set X, the maximal element belongs to
the boundary between the finite and infinite in the larger, atomic lattice
is not an
element of the sequence of rational numbers that defines it, so too the maximal
“element” may or may not be an element of the ideal of which it is the supremum. When it is
not, I shall also call such an element a boundary element. In the paradigmatic case of the ideal of all
finite subsets of some infinite set X, the maximal element belongs to
the boundary between the finite and infinite in the larger, atomic lattice ![]() .
.
This
is part of a longer thesis advancing a refutation of strong AI. To download the thesis visit: -
For an introduction to the work as a
whole visit: -
Introduction
to Poincare’s thesis by Peter Fekete